Tests

First a family update, then some thoughts on Covid tests.

Update

We tested positive for Covid on Monday. We're doing well. Our experience is matching up with the common reports about Omicron – a mild cold so far.

Emma and my symptoms started in earnest on Wednesday. Stuffiness, sneezing, coughing, some fatigue. It's nowhere near the worst cold we've ever had. I doubt we would have missed work or school for these symptoms in pre-pandemic days. I felt sick for 2.5 days, at some point last night I realized I hadn't sneezed or coughed in several hours, and when I woke up this morning I had a distinct feeling of "it's gone." Now it's the phlegm purging phase. Emma's experience seems to be tracking with mine.

Rachel's a day behind us (more on that in a bit). Her symptoms started in earnest on Thursday, she slept most of Friday, and she's feeling better this evening.

Julia started showing her first signs of being sick today. She took an abnormally epic nap this afternoon, and was cranky at bedtime. The odds of her being fine are heavily in her favor, but we'll feel better in a day or two.

Update: she woke up at 5:30am with a 103.8 fever and a cough 🙁.

Update 2: The fever went away after a day. She's super congested, but doing okay.

Today is day six of quarantine. Quarantine's been harder than the sickness, despite having so much practice in 2020. Emma's got a lot of energy. Rachel hasn't left the house this week. I've left to walk the dog and move the car. We ordered groceries on Monday, but we've mostly been living off of food and treats delivered to us by our friends, Kat, Hannah, and Nissa. (Thank you!)

Many of you have called, emailed, texted, and DMed to check in on us. Thank you! It's meant a lot to us. We're looking forward to re-entering society in the near future, and putting our newfound immunity to work.

Tests

On Monday, I wrote:

Turns out, the problem with antigen tests is false-negatives, not false-positives. "If a rapid test says you've got it, you've got it."

That quote felt too unnuanced to be accurate, but I sent it anyway. My friend Eric Liu wrote back right away and said,

"I rapid tested positive and PCR came back negative. Both tests were administered back to back at a testing facility. False positive on rapids are definitely a thing. There's a lot of conflicting anecdotes about it online and even among medical professionals."

Indeed....

Rachel, Emma, and I tested positive at home on Monday. Emma's positive line showed up strong and quick. Rachel and my lines were faint and, looking back, probably showed up after the 15 minute mark. We got PCRs that afternoon, and the results came in Wednesday morning.

Emma and I were PCR positive but Rachel and Julia were negative!

On Monday, Emma and I twice tested positive for one of the most contagious viruses in history. Rachel lives with us, and developed symptoms on Thursday. So... whatever her status was on Monday, she's got Omicron now (though, it does extend our quarantine by a bit).

Prior to this experience, my mental model has been "Antigen tests sometimes miss cases but are pretty accurate overall, and PCRs are the word of Fauci." Recently I've found myself a lot more interested in "what does a positive result actually mean?"

I got another reply this week that helped me better understand that. Luke Preczewski is one of the guys I've been playing poker with for fifteen years. Today he runs the Miami Transplant Institute, which in 2019 set the high score for most transplants performed by any hospital in the United States. Luke's been a brilliant source of nuanced knowledge throughout the pandemic – getting his take on things has been one of the best parts of rebooting our game.

Here's Luke's reply, reposted with his permission:

You mentioned antigen testing errors, and I thought you might find this interesting if you don't already know it. This is something that huge swaths of people get wrong all the time. And I don't mean population-wide, I mean smart people. Doctors and nurses, etc....

Tests are evaluated on their sensitivity and specificity.

Sensitivity is the true positive rate, or the ability to avoid a false negative. So if you test 1000 samples of people known to have a disease, and 950 test positive, the test has 95% sensitivity.

Specificity is the true negative rate, or the ability to avoid a false positive. So if you test 1000 samples of people known not to have a disease, and 100 test positive, the test has a specificity of 90%.

High sensitivity, but weaker specificity is good for ruling out disease, but bad for ruling it in, because a positive person is highly likely to test positive while a negative person might also test positive. And vice versa, of course. However, what many people miss about this is that those rates are calculated by testing known positives and negatives and seeing how accurate the test is. This makes sense. But that's not how tests are used. They are implemented to test unknown people.

People equate a sensitivity with the likelihood a positive result means you have the disease. It isn't, unless the entire population being tested has the disease. Similarly, a specificity does not tell you a likely negative result is accurate unless the entire population doesn't have the disease. Those concepts are different rates, called the positive predictive value (PPV) and the negative predictive value (NPV).

As no one tests populations already known to have or not have a disease (other than for validating tests...), you have to adjust for how prevalent a disease is in the population being tested. That's the piece people miss. So you can only determine PPV and NPV from Sensitivity and Specificity with an estimate of the prevalence of the disease in the population being tested.

For instance, if a COVID test has a 95% sensitivity and a 90% specificity, and the population of people who are going to get COVID tested are 20% positive, let's say 1000 people get tested: 1000 people with 20% prevalence means 800 true negative patients and 200 true positive patients.

The 200 true positive patients will have the result from the 95% sensitivity. 95% of them (190) will have accurate positive results. 5% of them (10) will have false negatives.

The 800 true negative patients will have the result from the 90% specificity. 90% of them (720) will have accurate negative results. 10% of them (80) will have false positives.

So 190 + 80 = 270 people will test positive, and 190 of those are actual positives, for a PPV of 70%. Meanwhile, 730 people will test negative, 720 of whom are legit negative, for a NPV of 98.6%. So while the test is more accurate in the positive group, because so many more people being tested are negative, the NPV is way higher.

Now let's say we're testing when rates are much lower. Say 2% of people getting tested have COVID. Repeat the above for another 1000 people: 980 negatives by 90% gives 882 accurate negatives and 98 false positives. 20 true positives by 95% gives 19 accurate positives and 1 false negative. So the PPV is 19/117 = 16%.

So this highly accurate test for identifying positives gives a test that, if positive, is only right 16% of the time. Meanwhile its NPV is 99.9%.

What this also means, is that while the sensitivity and specificity of a test don't change, the PPV and NPV change with the disease prevalence. Super important in a wave pandemic. The PPV of a test in Miami today is way higher than one in Johannesburg.

It also means you have to look who gets tested. If you look at the tests being given to people who want to get on an international flight, the actual prevalence is way lower than people who go to an ER with symptoms. So the PPV in those two situations is quite different.

I think I'm starting to grok this idea. "If a rapid test says you've got it, you've got it" – that's too simple of a statement. A better framework would be, "If a rapid test says you've got it, there's a XX% chance you've got it."  That XX% is the Positive Predictive Value. And the PPV varies depending upon the prevalence of infection amongst the group being tested.  

Since Luke introduced me to this concept, I've found playing with the sliders on this page interesting and helpful – seeing how the false positives and positive predictive value change at different levels of prevalence and sensitivity.

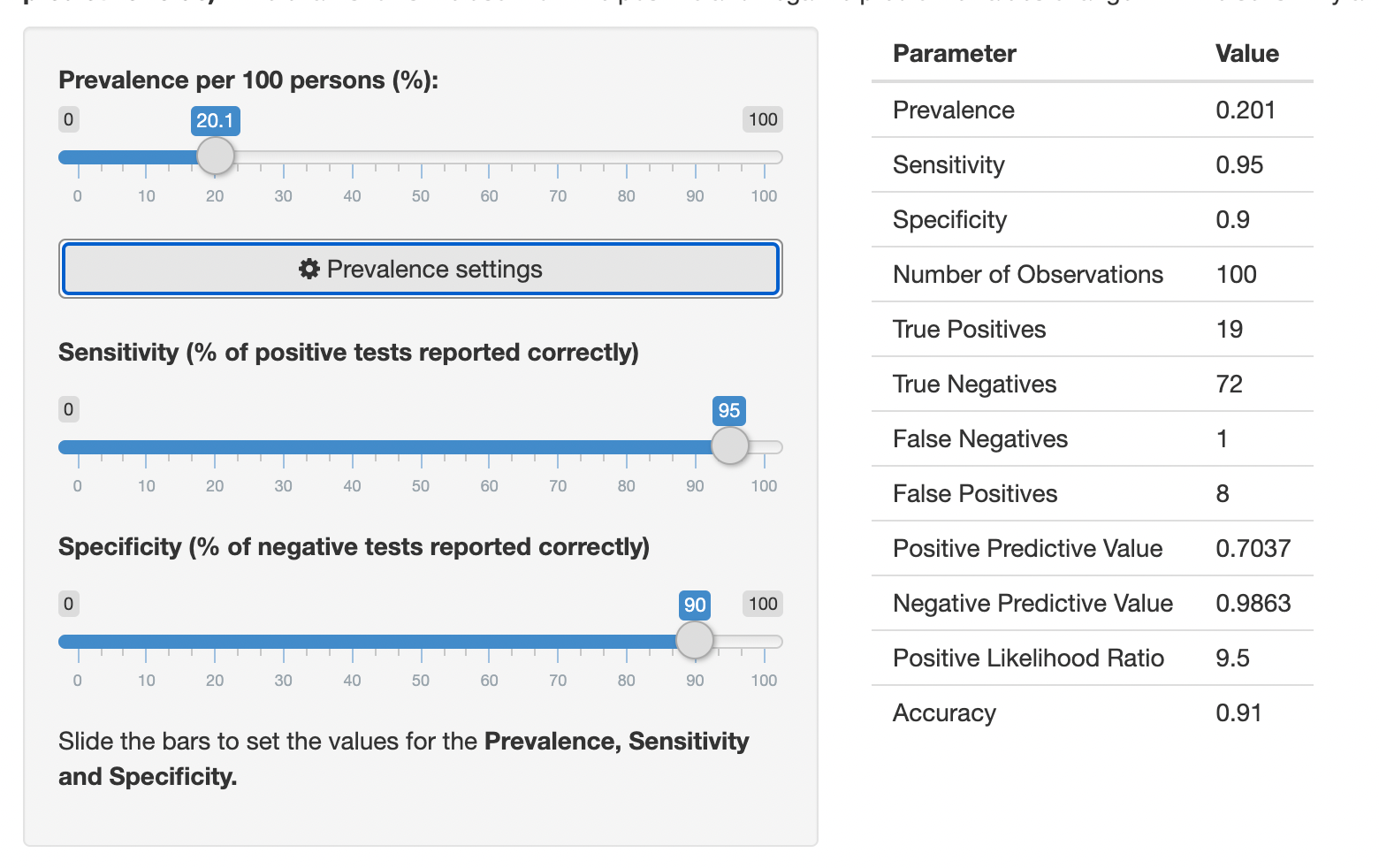
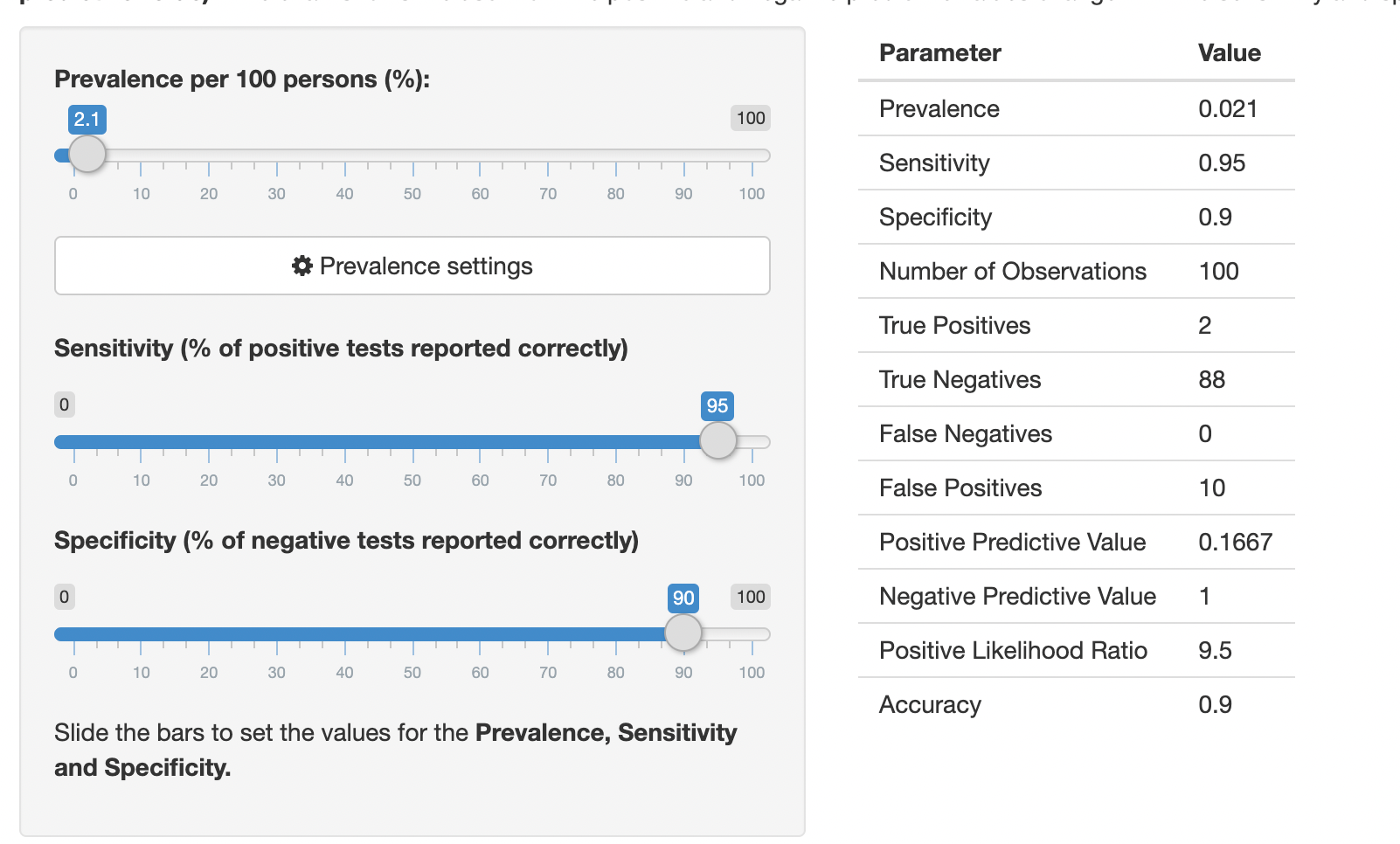
I can't say that this concept or its ramifications has fully clicked in my head yet, but I know that several of you in particular on this list are going to find this math fascinating, and I'd love to hear your thoughts on it.

Thank you for taking the time to write this up, Luke.

And thank you again to every one who's reached out and taken care of us this week. We're grateful to have so many folks who care about us.